Calculer la force de gravité
Calculez facilement la force de gravité ou force d'attraction gravitationnelle entre deux objets (planètes, atomes, chèvres, etc... bref tout ce que vous voulez) à partir de leur masse et de leur distance.
La gravitation universelle est une loi physique, énoncée par Isaac Newton en 1687, qui stipule que chaque masse attire chaque autre masse par une force en direction des centres de gravité de chacune d'elle. Cette force est proportionnelle au produit des deux masses et inversement proportionnelle au carré de la distance entre les centres de gravité de ces masses.
La force F est mesurée en Newton, m1 et m2 en kilogramme, d en mètre et la constante G est égale à 6,67408 x 10-11 Nm2kg-2.
La valeur de la constante gravitationnelle G a d'abord été déterminée avec une assez grande précision par l'expérience Cavendish menée par le scientifique britannique Henry Cavendish en 1798. Elle a depuis été affinée, mais reste cependant soumise à une petite imprécision.
Calcul de la force d'attraction gravitationnelle
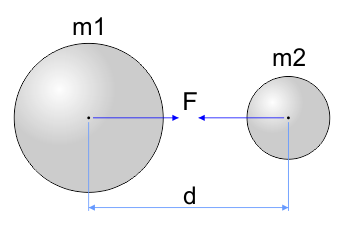
Notez que la distance à prendre en compte est celle entre les deux centres de gravité des masses.
Formule de calcul de la gravité
Pour calculer la force de gravité à partir de deux masses et de leur distance, il suffit d'appliquer la formule suivante :
F = G x m1 x m2 / d2
La force (en Newton) est égale à la multiplication de la constante G et des deux masses (en kilogramme), divisée par le carré de la distance (en mètre).
La constante gravitationnelle G
Selon les différentes expériences réalisées pour déterminer la constante gravitationnelle G, les résultats varient légèrement. La constante moyenne retenue par le Comité de données pour la science et la technologie (CODATA), dans le Système International d'Unités, est : 6,67408 x 10-11 m3kg-1s-2 (ou Nm2kg-2), avec une imprécision de + ou - 0,00031.
Multiples de l'unité Newton
Précision sur les multiples et sous-multiples de l'unité Newton utilisés dans le formulaire ci-dessus :
- Dyne (dyn) : 0,00001 N soit : 10-5 N
- Millinewton (mN) : 0,001 N soit : 10-3 N
- Centinewton (cN) : 0,01 N soit : 10-2 N
- Décinewton (dN) : 0,1 N soit : 10-1 N
- Newton (N)
- Décanewton (daN) : 10 N soit : 101 N
- Hectonewton (hN) : 100 N soit : 102 N
- Kilonewton (kN) : 1000 N soit : 103 N
- Meganewton (MN) : 1000 000 N soit : 106 N
- Giganewton (GN) : 1000 000 000 N soit : 109 N
Force de gravité entre la Terre et le Soleil
La force d'attraction entre la Terre et le Soleil est facilement calculable avec le formulaire ci-dessus.
Essayez et vous vous rendrez compte de la force colossale de cette attraction. C'est grâce à celle-ci que la Terre reste en orbite autour du Soleil, car elle est la force centripète, l'exacte opposée de la force centrifuge, elle aussi colossale, de la Terre en rotation autour du Soleil.
Entrez les valeurs suivantes dans le formulaire de calcul :
- Masse de la Terre : 5.972E+24 kg
- Masse du Soleil : 1.9891E+30 kg
- Distance Terre - Soleil : env. 150 Gm (150 000 000 km)
- Précision : 0 (ou + si vous êtes très très tatillon
 )
)
- Unité du résultat : À vous de voir. Le daN permet de se donner une idée assez précise, puisqu'il représente, en pratique, le poids d'une brique de lait dans la main.
Les nombres 5.972E+24 et 1.9891E+30 peuvent être directement copiés-collés dans les cellules correspondantes. Le moteur de calcul comprenant l'expression 5.972E+24 comme signifiant 5,972 x 1024.
Force d'attraction de deux boules de pétanque
De la même manière, nous pouvons calculer l'attraction réciproque de deux boules de pétanque. Sachant qu'une boule de pétanque a une masse comprise entre 680 et 730 grammes et que la distance minimale entre les centres de gravité est égale à l'addition de leurs rayons respectifs, soit au total entre 72 et 75 mm.
Essayez et comparez avec le résultat de celui de la Terre et du Soleil. Un conseil, utilisez la plus petite unité de résultat, soit le Dyne et au moins 5 chiffres après la virgule pour commencer à voir une bribe du résultat. Bien que très proches les boules de pétanques ont du mal à rivaliser avec leurs grandes sœurs  .
.
L'attraction terrestre et vous-même
Calculez l'attraction réciproque de la Terre et vous-même. Entrez la masse de la Terre (5.972E+24 kg) et votre poids - qui soit dit en passant n'est pas votre poids, mais votre masse - puis sélectionnez l'unité de résultat, soit en Newton (N) ou en décanewton (daN) et vous obtiendrez un poids proche du vôtre, celui dû à la manifestation de l'attraction terrestre avec vous-même.
Il est à noter que le résultat de cette force (ou poids) est plus important que celle (ou celui) que vous ressentez, notamment parce que la rotation de la Terre sur elle-même tend à vous éjecter du sol et donc à réduire votre poids. D'autres facteurs entrent en ligne de compte, tels que l'attraction lunaire et solaire, et donc l'heure de la marée, etc... Mais arrêtons-nous là, avant d'en arriver à l'âge du capitaine.
La loi de la gravitation universelle
En 1687, Isaac Newton émet l'hypothèse que tout objet présent dans l'univers est soumis à l'attraction de n'importe quel autre objet présent dans ce même univers. Plus les corps sont massifs et proches l'un de l'autre, plus cette force d'attraction est importante. C'est cette force qui relie la Lune à la Terre et la Terre au Soleil et c'est cette même force qui fait tomber les objets au sol lorsqu'on les lâche. Il en tire une loi physique: la loi de la gravitation universelle.
La légende veut que Newton ait fait cette découverte alors qu'il somnolait paisiblement sous un pommier, en recevant sur la tête une pomme tombée de l'arbre (merci Monsieur Gotlib pour la scène que vous avez si magnifiquement immortalisée pour nous et qui grave à jamais cette légende dans nos esprits). Mais ce n'est pas tout à fait exact. S'il y a bien une histoire de pomme, c'est celle qu'il a vu tomber près de lui, alors qu'il rêvassait sous l'arbre. C'est alors qu'il pris conscience de l'attraction terrestre.
Liste des pages de calculs
Argent
Automobile
Construction
Conversion
Divers
Electricité
Hydraulique
Informatique
Mathématiques
Arithmétique
Géométrie
Calculs des surfaces
Calculs des volumes et de leurs surfaces
Calculs des développantes
Trigonométrie
Mécanique
Santé
Sciences
Usinage